today we will be covering 2 things:
today’s topic + a new question
solution to the question given in the last issue (you can find it here => get the ball rolling with R2-D2)
Tom Cruise was hanging onto the side of a military transport plane as it flew over the desert at a speed of 300 mph. he had just completed a top secret mission and was now being transported back to base. as the plane flew over the vast expanse of the desert, Tom couldn't help but feel a sense of exhilaration and freedom🙌
but Tom's sense of adventure got the best of him and he suddenly decided to jump out of the plane and experience the thrill of free-falling through the air. he let go of the plane and began plummeting towards the ground😱
as Tom fell, a second plane flying at an altitude of 1000 feet and a speed of 500 mph spotted him and decided to chase after him. the pilot of the second plane knew that it was their duty to rescue any fellow aviator in need, and Tom was in need of some serious rescuing🫡
the second plane quickly caught up to Tom and was able to safely retrieve him before he hit the ground. thanks to the quick thinking and bravery of the second plane's pilot, Tom was able to walk away from this daring escapade unscathed🤩
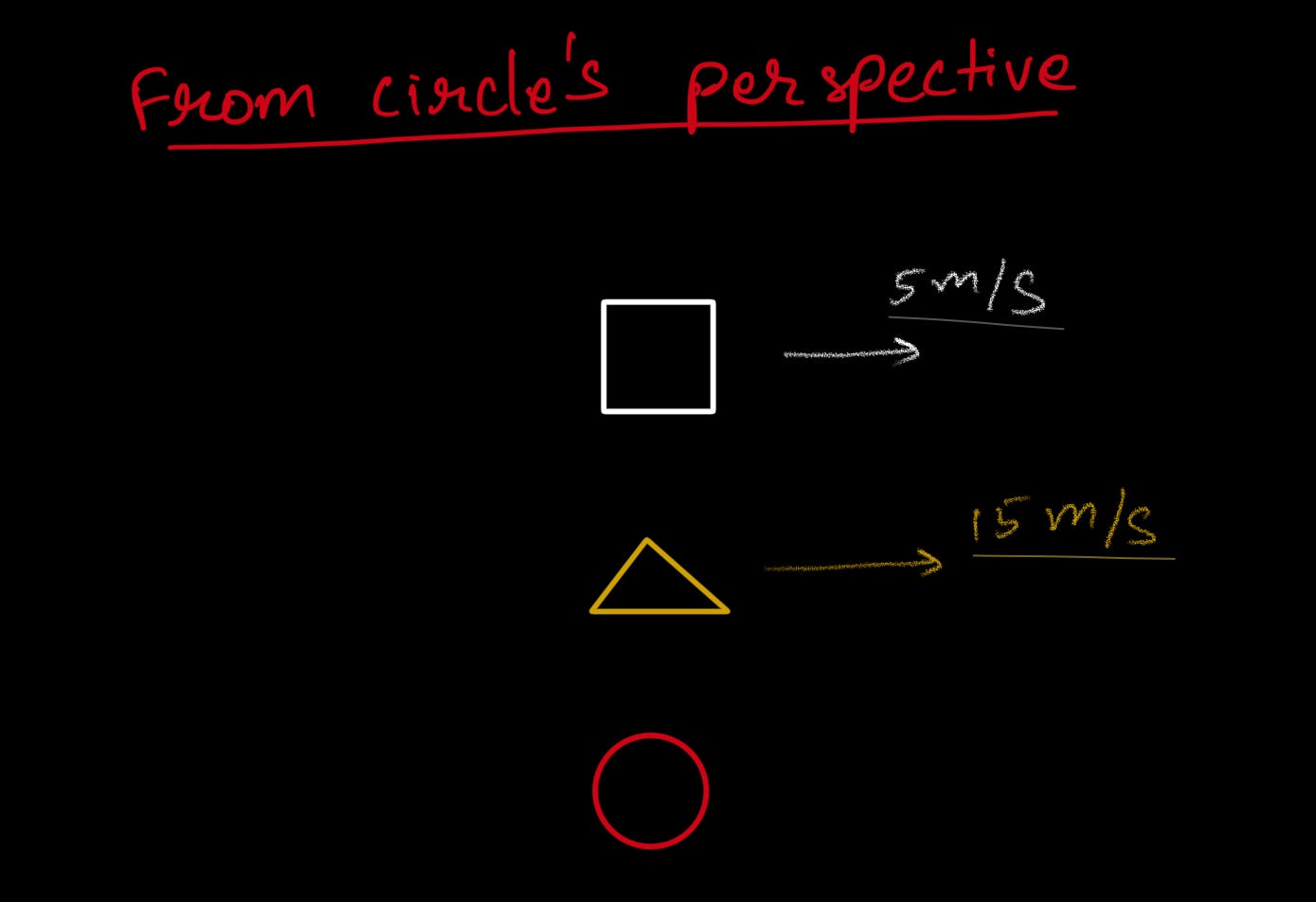
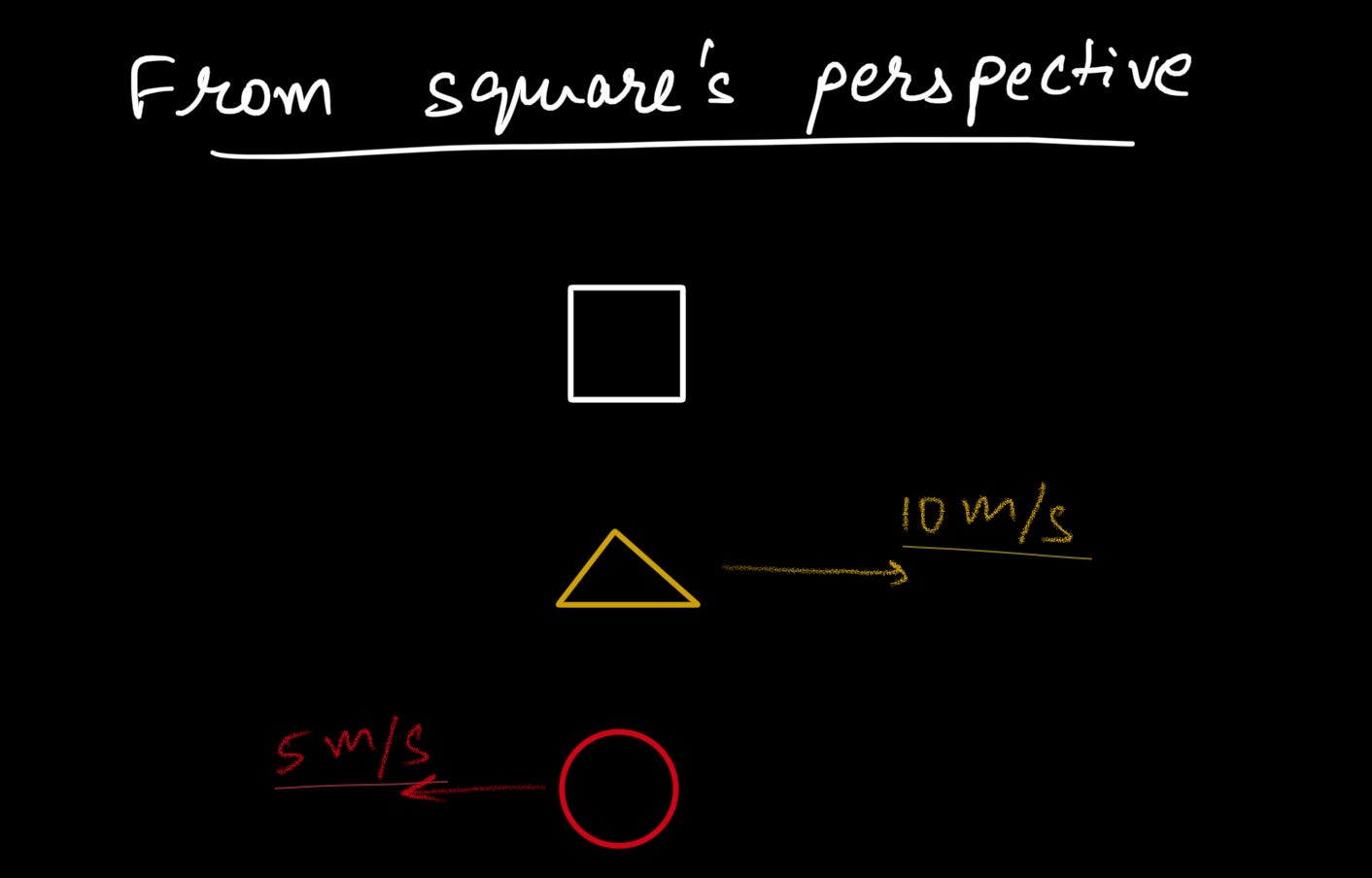
the thing with physics is, it depends on the person who’s looking at the given scene. let’s take an example to understand this.
for an astronaut watching the earth from the moon, it’ll seem as if the earth is rotating. but for a person on the earth, it’ll seem as if the earth is stable.
see the difference in perspective here?
this concept is called relative motion. it doesn’t have separate formulae tbh, but we need a lotta imaginative skills to understand which POV we need to take while looking at a situation.
a very simple example to illustrate relative motion:
when we see a scene from an object’s perspective, the object is usually at rest
let’s see an irl situation and break it down😈
Bugs Bunny on a boat
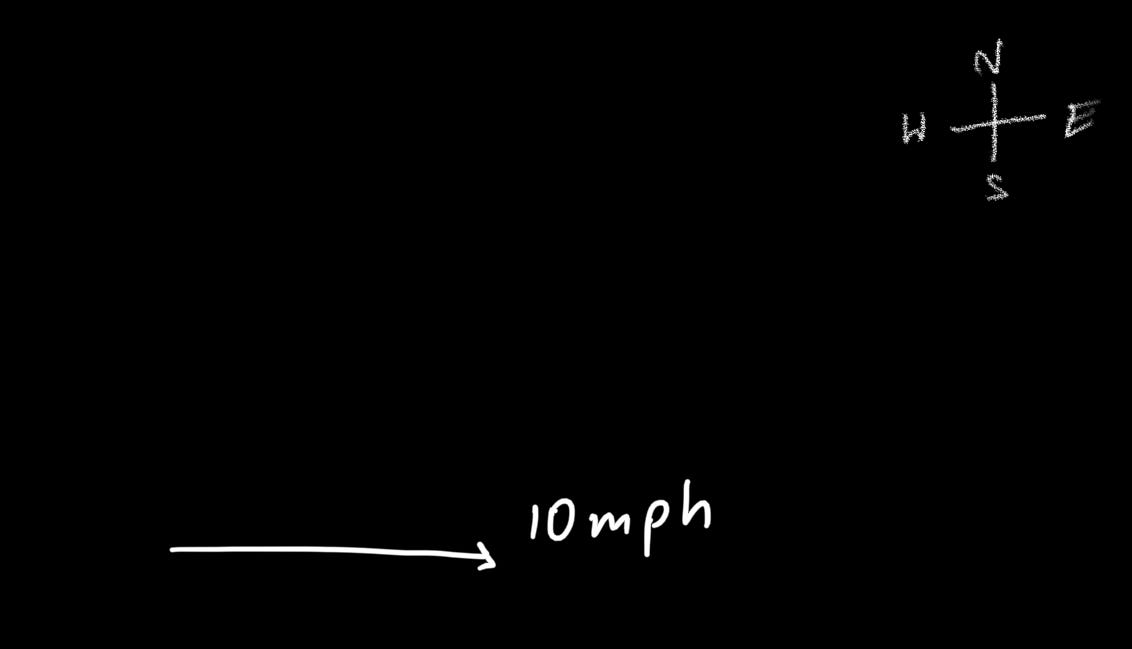
Bugs Bunny (from Looney Tunes) is sitting on a boat that is floating on a lake. the boat is traveling at a speed of 10 mph due east. he starts running around on the boat at a speed of 5 mph due north. what is his speed and direction relative to the shore?
solution:
the boat is traveling at a speed of 10 mph due east, which can be represented as a vector pointing in the east direction with a magnitude of 10 mph.
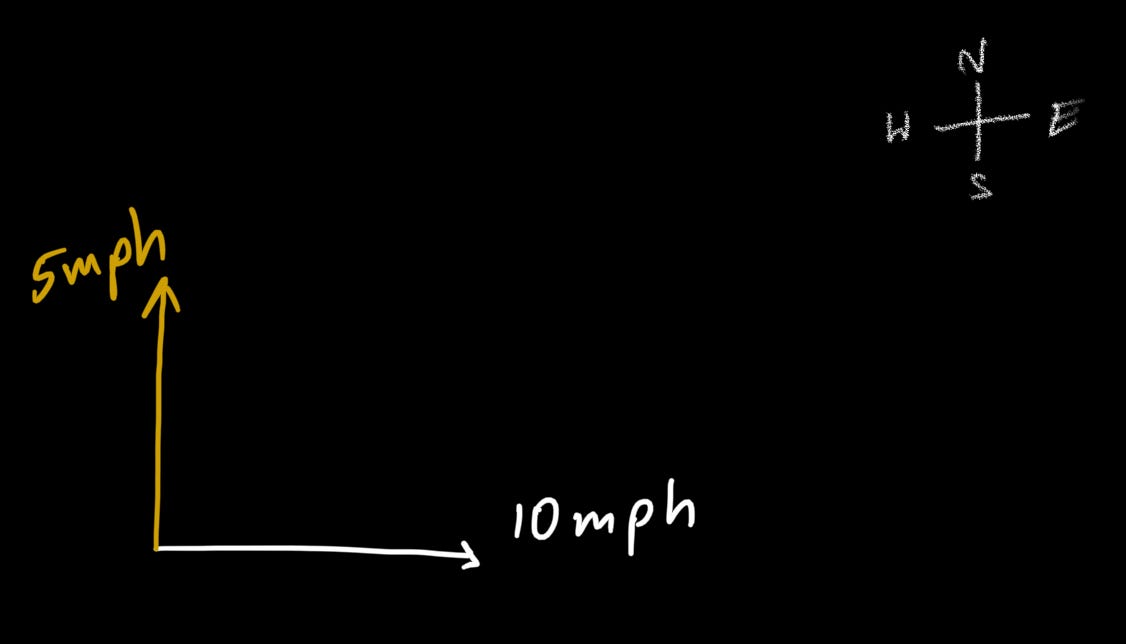
the bunny is traveling at a speed of 5 mph due north, which can be represented as a vector pointing in the north direction with a magnitude of 5 mph.
to find the bunny's speed and direction relative to the shore, you can add these two vectors together using vector addition. the resulting vector will point in the direction of the bunny's motion relative to the shore and will have a magnitude equal to the bunny's speed relative to the shore.
using a vector addition diagram, you can see that the resulting vector points in the northeast direction and has a magnitude of about 11.18 mph.
this means that the bunny's speed relative to the shore is about 11.18 mph and its direction is about 45 degrees north of east.
now let us convert the Tom Cruise story given above into a question:
Tom Cruise is hanging onto the side of a military transport plane as it flies over the desert at a speed of 300 mph. he then jumps out of the plane and begins free-falling towards the ground. at the same time, a second plane is flying towards Tom at a speed of 500 mph at an altitude of 1000 feet. how long does it take for the second plane to catch up to Tom?
ps: my diagrams are a lil weird, sowwy 😭
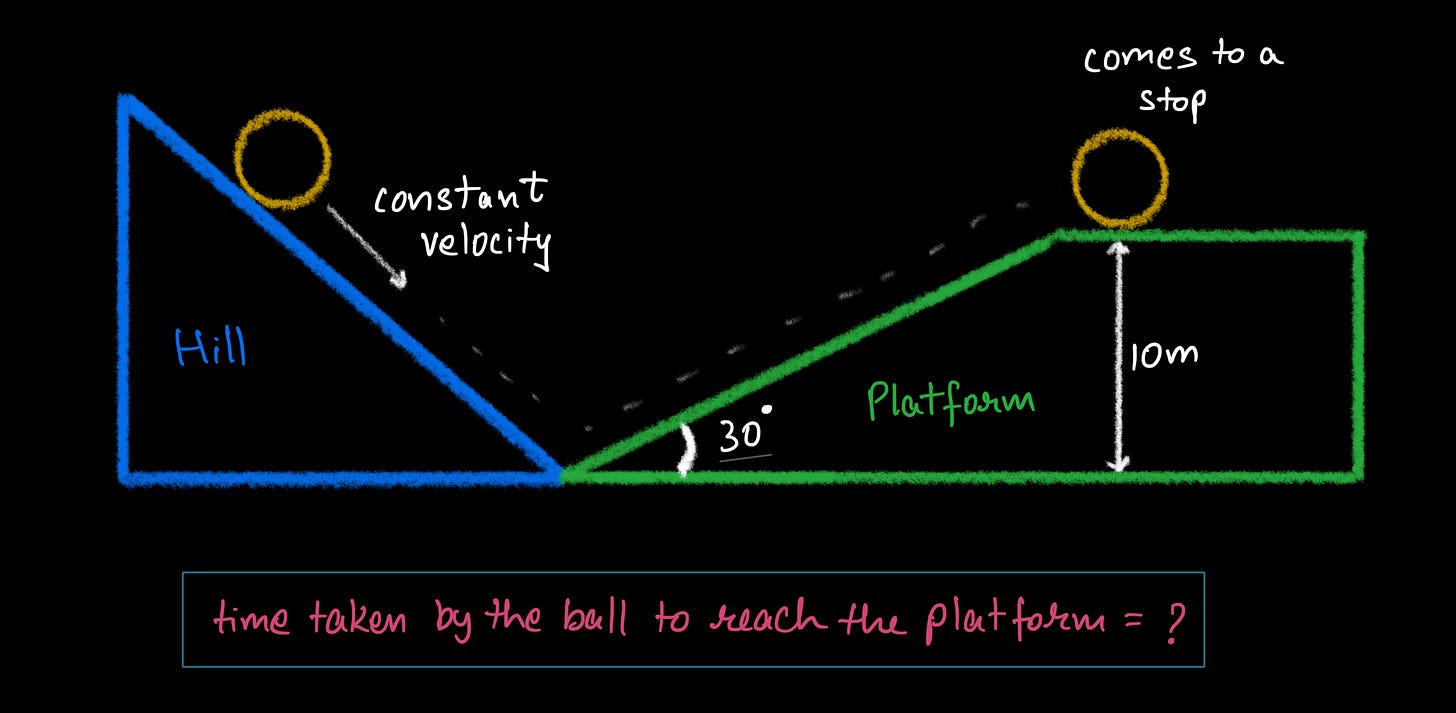
solution for the R2-D2 question
steps involved:
list out given information
constant velocity = v
displacement = 10m
angle of incline = 30 degrees
choose which equations of kinematics to use based on what’s given and what’s asked in the question
need to find time taken by the ball
from the angle of incline we can find the acceleration that’s acting on the ball (by breaking down the components of acceleration)
plug in values and solve the equations
solution:
first we find the acceleration of the ball along the ramp. for that, we isolate the ball from the scene and split the acceleration due to gravity to its components
since i’m at the limit for this issue, see ya next week!
bubye!










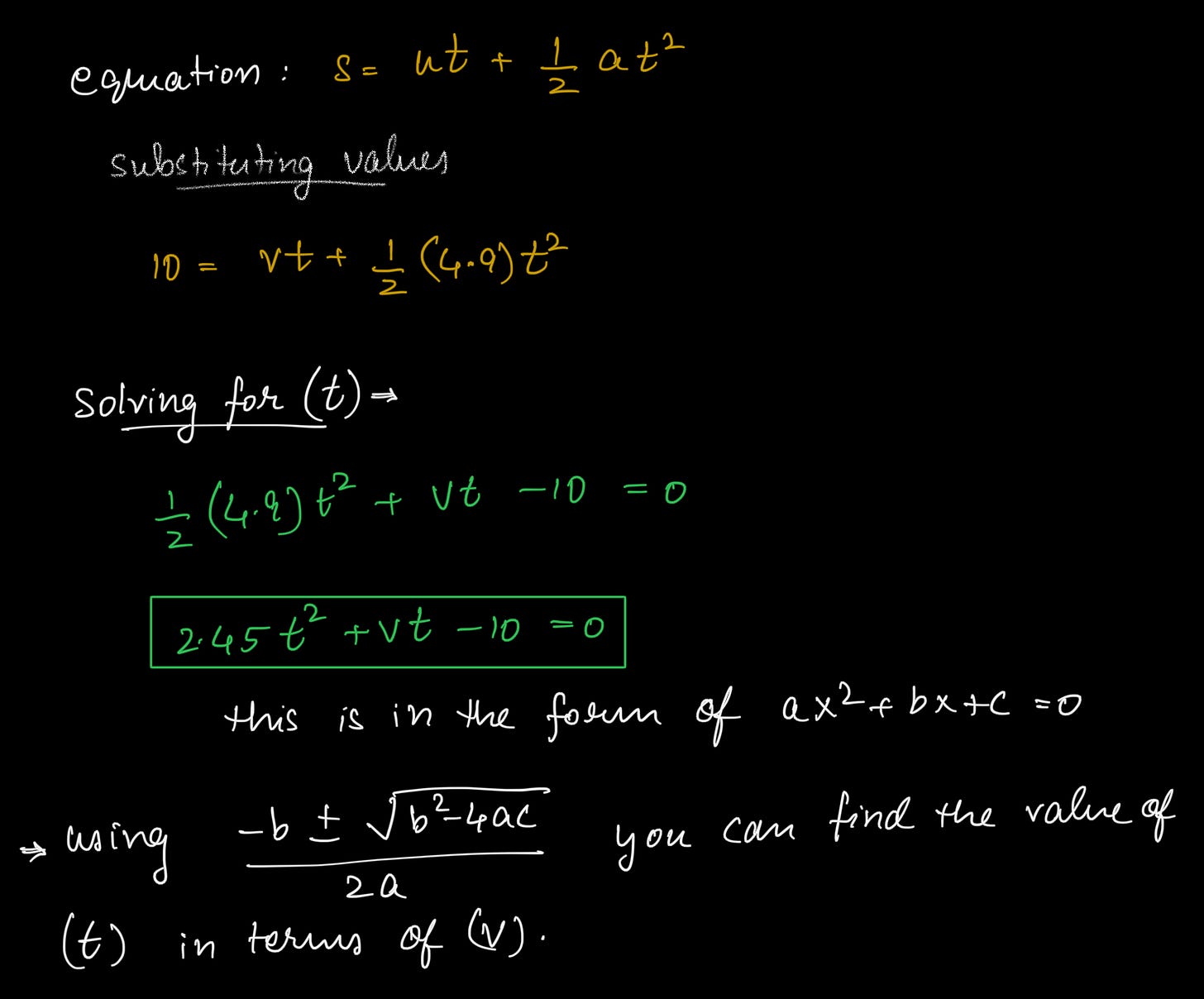
pretty crisp and clear, love it!